Un point de vue est limité en soi.
Il nous donne une vue unidirectionnelle du paysage.
Seul plusieurs points de vue complémentaires d’une même réalité mènent à l’accès et à la connaissance des choses.
Plus ce que l’on veut comprendre est complexe, plus il est important d’avoir plusieurs paires d’yeux, pour que les faisceaux de lumière convergent et que l’on puisse voir l’Un à travers la multiplicité. C’est la nature même d’une vision authentique : rassembler des points de vue déjà connus et en montrer d’autres, inconnus jusqu’alors, en nous apprenant qu’en fait, ils font tous partie du même Tout,
Alexandre Grothendieck
Nous affirmons souvent que la science officielle arrive à comprendre et à expliquer ce que les anciens savaient déjà depuis longtemps à travers l’intuition ou par une sorte de révélation. C’est vrai, mais la science a des temps et des modalités différents pour affirmer les mêmes vérités que les anciens. Son processus est beaucoup plus lent et laborieux. Un chemin fait de travail acharné et méticuleux et de petits pas l’un après l’autre, des pas bien plantés au sol car pour regarder le cosmos, Uranus (le ciel ordonné des anciens), il faut avoir une base solide sur laquelle s’appuyer [1].
Un exemple simple pour nous comprendre. Nous avons tous ‘l’intuition’ que 1 + 1 = 2. L’arithmétique que nous étudions à l’école nous le dit, mais aussi notre expérience quotidienne, notre connaissance empirique. Mais pour la science, ‘l’intuition’ ne suffit pas, la science procède par ‘démonstrations formelles’ et la preuve formelle que 1 + 1 = 2 occupe les 300 premières pages des Principes Mathématiques de Whitehead et Russell, un ouvrage monumental dont l’objectif (infructueux) était de formaliser les fondements sur lesquels reposent toutes les mathématiques. Pourquoi tant d’efforts pour dire que 1 + 1 = 2 ? Parce qu’il faut d’abord formaliser les acteurs en présence.
Qu’est-ce que le « 1 » ? Que signifie « 2 » ? Qu’est-ce que « + » ? Et qu’est-ce que « = » ? Cela peut sembler trivial, mais lorsque Whitehead et Russell se sont posé ces questions, un gouffre d’une profondeur inattendue s’est ouvert devant eux, et pour commencer à répondre à ces questions, il était nécessaire d’avoir un langage commun avec lequel définir les concepts de base. Ce langage commun dans lequel toutes les mathématiques peuvent être exprimées est la « Théorie des Ensembles » de Cantor Frege. Vers le milieu du siècle dernier, Mac Lane a étendu ce langage en fondant la « Théorie des Catégories », qui a donné beaucoup plus d’expressivité aux mathématiques et à ses différentes disciplines telles que la géométrie, l’algèbre ou la topologie. Dans les années 1960, Grothendieck a encore étendu cette théorie, la généralisant et l’amenant à son essence en introduisant les concepts de « Raison » et de « Topos ». Mais au départ, afin de prouver que 1 + 1 = 2 et de répondre aux questions pas du tout triviales posées ci-dessus, Whitehead et Russel ont utilisé la théorie des ensembles, et c’est ainsi que « 1 », dans les Principe Mathématiques, est « l’ensemble de tous les ensembles ne contenant qu’un seul élément ». De même, « 2 » est « l’ensemble de tous les ensembles contenant deux éléments ». Le « + » devient une opération d’union logique entre ensembles et le « = » est un concept non trivial d’équivalence qui, avec Grothendieck et Morita, atteindra son expression maximale de beauté et d’élégance.

Alexandre Grothendieck, surnommé l’Albert Einstein des mathématiques, a utilisé l’instrument d’abstraction pour sonder les fondements des mathématiques de plus en plus profondément jusqu’à ce qu’il en atteigne le cœur. Pour lui, tout dilemme pouvait être simplifié si on l’examinait dans son essence. Il ne s’intéressait pas aux nombres, aux courbes, aux lignes ou à tout autre objet mathématique particulier, mais à la relation entre eux. Il avait une sensibilité extraordinaire pour trouver l’harmonie entre les choses. L’un de ses plus grands coups de génie a été d’élargir la notion de point. Celui-ci cesse d’être une position sans dimension et devient animé d’une structure interne complexe qui contient un univers infini. C’est ainsi qu’est né le concept de Topos. Regarder le monde et la réalité à travers le prisme du Topos revient à s’abstraire à un point tel que les mots du langage naturel (que nous avons inventée, alors que ce n’est pas le cas pour les mathématiques, comme Platon l’avait déjà deviné) ne suffisent pas à décrire l’expérience. C’est comme observer le « tout » du point de vue du « non tout », ou le fini du point de vue du non-fini ou de l’Infini, dé-fini dans ces pages comme le « voile de l’Absolu ».
Ce sont des lieux de réflexion fascinants et enchanteurs, mais aussi extrêmement dangereux. Grothendieck lui-même a écrit : « même en mathématiques, certaines choses devraient rester secrètes à jamais, pour notre bien à tous ». Une telle affirmation peut sembler exagérée, mais tout comme en physique il existe des monstres cosmiques tels que les trous noirs qui déchirent littéralement l’espace et engloutissent tout, même le temps, en mathématiques il existe des démons capables d’engloutir et d’anéantir jusqu’à la pensée. Des monstres qui peuvent rendre fous des savants de génie, comme ce fut le cas de Gödel (dont nous parlerons dans un instant) ou de Grothendieck lui-même, qui a écrit : « l’humanité vit dans l’ombre d’une nouvelle horreur », celle du « sommeil de la raison » (F. Goya). Pourtant, au-delà des limites de l’esprit définies comme concrètes par les Enseignements ésotériques, d’autres vibrations attendent d’être reçues par les niveaux supérieurs de l’intelligence sage.

Et en parlant d' »essence », il faut faire attention à quel niveau on cherche le cœur des phénomènes que l’on veut analyser. Un exemple : on dit souvent que le Son et la Lumière ont la même essence. Mais en tant que phénomènes physiques, la seule chose que le Son et la Lumière ont en commun est qu’il s’agit de deux phénomènes vibratoires. Les analogies s’arrêtent là.
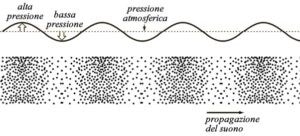
Le son est la vibration moléculaire d’un milieu physique, qu’il soit gazeux, liquide ou solide ; en fait, dans l’espace vide (c’est-à-dire, pour la Sagesse Antique, simplement plus subtil, présentant l’Espace comme vivant ou plein de Vie), en dehors de l’atmosphère terrestre, règne le silence le plus profond, inaudible par les moyens physiques ordinaires.
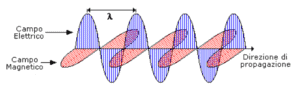
La lumière est la vibration de quelque chose de complètement différent du son, c’est la vibration d’un champ : le champ électromagnétique qui peut se propager même dans le « vide » de l’espace profond ; et l’Univers lui-même a une vibration d’une nature encore différente du son et de la lumière, c’est la vibration d’un autre champ : le Champ de Higgs, responsable de tout ce qui est en manifestation, y compris l’Univers lui-même, qui à son tour est une caractéristique manifeste du champ gravitationnel. En d’autres termes, affirmer que le son et la lumière ont la même essence présuppose une connaissance partagée du sens du mot Essence, qui n’est pas celui de leur manifestation physique, où les deux entités ne sont pas interchangeables. En philosophie occulte, les idées de Son et de Lumière ne désignent donc pas leurs contreparties phénoménales ou physiques, mais plutôt la Vibration de la Vie aux différents niveaux de la Substance spatiale.

Comme Grothendieck, Kurt Gödel s’intéressait également à l’essence en tant que vérité abstraite ou cœur des mathématiques, et pour rechercher cette essence, il a tourné la puissance du formalisme mathématique vers les mathématiques elles-mêmes [2]. Ce qu’il a découvert a marqué à jamais le monde de la logique et des mathématiques, en trouvant dans son « essence » la même nature d' »indétermination » [3] qu’Heisenberg avait trouvé dans les fondements de la Physique quelques années plus tôt. En termes simples, Gödel a découvert que dans les systèmes mathématiques formels, tels que l’arithmétique, il existe des énoncés sur les nombres qui sont vrais, mais dont la vérité ne peut être prouvée à l’aide de l’arithmétique elle-même. Ainsi, tout système formel, par exemple tout système de nombres, est par nature incomplet (c’est pourquoi le projet de Whitehead et Russell a échoué). Il présuppose l’intervention d’un plan d’observation ou de compréhension autre que celui du raisonnement intellectuel de la recherche mathématique.
Les mathématiques, maqhmatikóV, en tant que terme, se réfèrent à tout ce qui est lié à l’étude, à l’apprentissage et à la connaissance, mais Grothendieck, Gödel et Heisenberg ont marqué des limites au-delà desquelles nous ne sommes pas autorisés à aller dans cette connaissance intellectuelle. Il existe des « horizons d’événements » au-delà desquels tout – l’espace, le temps, la pensée – perd son sens. Ces grands penseurs nous ont dit que, quelles que soient la profondeur et la passion de nos études, il y aura toujours des vérités qui nous seront interdites dans cette manifestation, et cela la science l’a appris depuis les années 1930. Quels que soient les efforts de l’humanité, il existe des barrières, des voiles, au-delà desquels notre regard physique ne peut aller. Nous devons l’accepter et cela s’applique à tout type d' »Enseignement » appris uniquement à certains niveaux de l’esprit. Cela ne signifie pas que la science est limitée par rapport à l’intuition ou à la possibilité de développer des outils de perception de tout ce qui « résonne avec nous d’une manière ou d’une autre ». Les limites cognitives sont universelles ou proportionnelles aux différents niveaux de « réalité » ou de conscience, et les enseignements sapientiels affirment que : « L’humanité ne pourra accéder à certains niveaux de compréhension que lorsqu’elle sera prête. »
Le langage utilisé par la science pour décrire ces limites est très compliqué, pour quelques « disciples », tout comme le langage de l’ésotérisme qui est réservé à ceux qui se consacrent à son étude. Nous devons tous, scientifiques et ésotéristes, nous efforcer de faire en sorte que ces langages convergent de plus en plus et que les scientifiques ne considèrent pas les ésotéristes comme des charlatans et que les ésotéristes ne considèrent pas les scientifiques comme des aveugles et des sourds. Comme l’a écrit Grothendieck dans la citation au début de cet article, ce n’est qu’avec un regard commun que nous pouvons reconnaître que nous faisons partie du même Tout.
Il est important que, pour chaque discipline d’étude et de recherche, nous procédions avec ouverture d’esprit et curiosité, afin d’arriver à construire des ponts de pensée, des connexions et donc des langages communs qui respectent les catégories de sens de chaque « science », conduisant à cette unification de la connaissance et de l’étude que nous avons oubliée au fil des siècles.
[1] Ce que l’on appelle la « Méthode Scientifique » repose sur l’observation du phénomène, l’élaboration d’une théorie à son sujet et la réalisation d’expériences pour vérifier l’hypothèse théorique.
[2] ”. C’est ce qu’on appelle un processus « métamathématique ».
[3] Il est impossible ici d’expliquer de manière exhaustive la formidable découverte de Gödel que sont les « théorèmes d’Incomplétude Syntaxique« . En langage courant, on pourrait résumer son résultat en disant que tout système formel S dans lequel une certaine quantité d’arithmétique peut être développée et qui satisfait à certaines conditions minimales de cohérence (pas de contradictions) est incomplet : on peut construire un énoncé arithmétique élémentaire A tel que ni A ni sa négation ne soient prouvables dans S. En effet, l’énoncé ainsi construit est alors vrai (au sens où il est possible) puisqu’il exprime son indémontrabilité dans S, par une représentation en arithmétique de la syntaxe de S. De plus, on peut construire en arithmétique un énoncé C qui exprime la consistance de S, et C n’est pas prouvable dans S si S est consistant.





